ERRABL
Estimation de Ressource dans le RAz BLanchard
© Cristian Palmer @cristianpalmer Unsplash
Axe Environnement
Mathématiques
∩ Energie
Aperçu
Accélérer le développement de la filière hydrolienne en améliorant la méthode d’estimation de la ressource grâce à l’analyse numérique, l’assimilation de données et la méta-modélisation.

(https://www.flowatt.fr/)
Mots clefs
Hydrolienne, analyse numérique, optimisation, assimilation de données, méta-modélisation, incertitudes, Raz Blanchard.
Coordination
- Julien Salomon (Mathématiques, équipe ANGE, INRIA)
- Jerôme Thiébot (Hydrodynamique, Laboratoire Universitaire des Sciences Appliquées de Cherbourg (LUSAC), UR 4253, Université de Caen)
Financement
- 553 200 € sur 48 mois (Projet scientifique lauréat de l’appel à projets 2024)
Résumé
Le projet scientifique ERRABL vise à améliorer nos connaissances sur la ressource hydrolienne d’un site où s’écoule l’un des courants les plus puissants du monde : le Raz Blanchard. Son exploitation est envisagée à court terme, les premières évaluations prévoyant le déploiement de fermes d’hydroliennes pouvant produire plusieurs centaines de mégawatts. Elle nécessite cependant une évaluation préalable précise de la ressource énergétique ainsi que des incertitudes associées.
Le projet scientifique ERRABL vise à contribuer aussi bien méthodologiquement que de manière pratique à une meilleure estimation de la ressource du Raz Blanchard en améliorant les outils existants basés sur un code numérique qui résout les équations de Saint-Venant (ou de Navier-Stokes) et des mesures de vitesse de courant effectuées sur site. Dans un premier temps, les membres du projet optimiseront le code principal en corrigeant certains termes paramétrés (turbulence, frottement…) avec des données disponibles. Cette approche implique de réaliser un apprentissage indirect, où la correction est déterminée à travers un schéma de simulation. Les membres du projet développeront une approche originale, consistant dans un premier temps à équilibrer les différentes erreurs (schéma, modèle, bruit…), de sorte qu’aucun calcul inutilement précis ne soit effectué. D’autre part, ils rechercheront un modèle correctif indépendant de la discrétisation. La stratégie se base sur une analyse a posteriori des erreurs et consiste à faire varier la discrétisation et le niveau de bruit artificiellement, pour déduire l’erreur de modélisation introduite par les termes paramétrés. Dans le cas d’une correction par réseau de neurones, les membres du projet accéléreront la détermination de la correction en s’inspirant de l’extrapolation de Richardson. Ils testeront également une stratégie consistant à corriger le code 2D par un apprentissage sur le code 3D. Ensuite, ils émuleront Telemac par un méta-modèle. Ce nouveau code, différentiable et rapide par définition, permettra d’augmenter massivement le nombre de simulations. Les membres du projet l’utiliseront pour quantifier les incertitudes et optimiser le placement des hydroliennes au sien du site. Ils travailleront sur le couplage du méta-modèle avec ces différentes procédures. Il s’agira en particulier d’étudier la propagation d’incertitudes, i.e., d’obtenir une procédure fournissant des probabilités de sorties à partir de probabilités d’entrées. Pour l’optimisation, il s’agira de vérifier que certaines propriétés, comme la stabilité ou le bilan énergétique, sont préservées. Enfin, ils appliqueront de manière concrète les outils développés. A l’issue de ce travail, les membres du projet disposeront d’un code Telemac du Raz Blanchard optimisé, c’est-à-dire plus précis et moins coûteux en temps de calcul, ainsi que d’un méta-modèle l’émulant. Ils auront identifié les processus physiques dont il faut améliorer la fiabilité pour mieux reproduire la dynamique des courants extrêmes. Ils auront également testé une méthode, transposable à d’autres sites, pour estimer les incertitudes. De plus, les membres du projet proposeront des recommandations sur le placement optimal des turbines au sein du site.
- Optimiser le code utilisé pour estimer la ressource en corrigeant des termes paramétrés
- Équilibrer les erreurs du code en utilisant l’apprentissage
- Développer un méta-modèle pour émuler le code d’estimation de la ressource
- Quantifier les incertitudes
- Optimiser le positionnement des turbines au sein du site hydrolien
- Analyse numérique
- Assimilation de données
- Apprentissage
- Incertitudes
- Optimisation
- Équilibrage des erreurs
- Code éléments finis
- Mesures de vitesses de courant
- Améliorer les connaissances sur la ressource du Raz Blanchard
- Augmenter les performances du modèle d’estimation de la ressource
- Proposer une méthodologie d’estimation des incertitudes sur la ressource
- Développer un outil d’optimisation du design des fermes hydroliennes
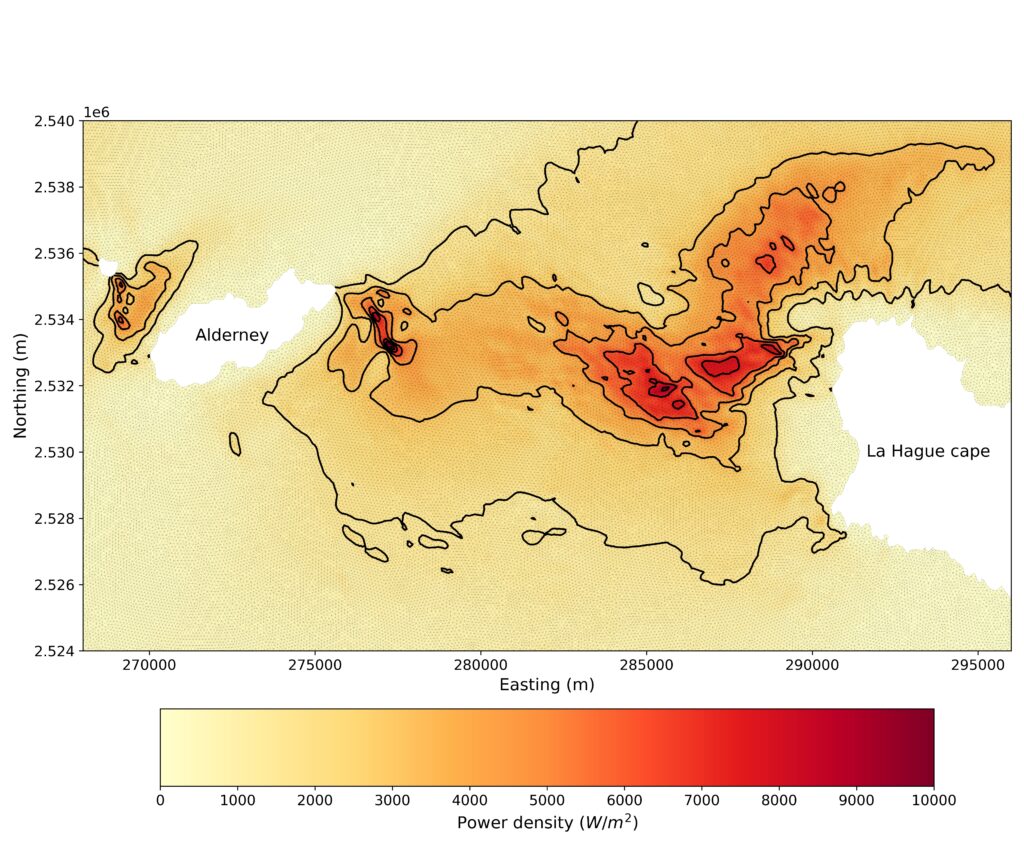
© LUSAC
Recrutements envisagés
- 2 doctorats
- 1 post-doctorat
Plus de projets

